Will man auf einem Rootserver parallel einen Apache und einen Node.js Server betreiben hat man das Problem das beide nicht einfach auf dem selben Port laufen können. Zwar ist es theoretisch möglich Node.js oder Apache auf unterschiedlichen Ports laufen zu lassen. Allerdings ist das bei Webserver unüblich und kann zu Problemen führen wenn bei einigen Benutzern nur der Port 80 in der Firewall geöffnet ist. Auch ist es damit nicht möglich nur eine bestimmte Subdomain unter Node.js zu betreiben.
In der folgenden Anleitung wird beschrieben wie man eine Subdomain unter Apache an einen Node.js Server weiterleitet, alles wurde unter Ubuntu erfolgreich getestet. Die hier vorgestellte Lösung ist performance-technisch nicht optimal aber einfach umzusetzen.
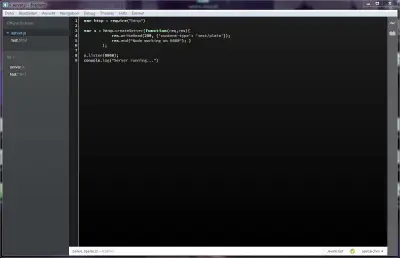
Hier der verwendete minimale Node.js Server:
var http = require("http");
var s = http.createServer(function(req,res){
res.writeHead(200, {'content-type': 'text/plain'});
res.end("Node working on 8080");
});
s.listen(8080);
console.log("Server running...") Für den Apache müssen über zwei zusätzliche Module installiert werden: sudo apt-get install libapache2-mod-proxy-html Danach müssen die beiden Module über sudo a2enmod proxy_http
sudo a2enmod proxy aktiviert werden. Die Virtualhost-Datei muss wie folgt aufgebaut sein:
<VirtualHost *:80>
ServerName tour.ragersweb.de
ServerAdmin webmaster@ragersweb.de
ProxyRequests On
<Proxy *>
Order deny,allow
Allow from localhost
</Proxy>
ProxyPass / http://localhost:8080
ProxyPassReverse / http://localhost:8080
</VirtualHost>
In diesem Beispiel werden alle Anfragen an die Subdomain bps.ragersweb.de an den unter Port 8080 laufenden Node.js Server weiterleitet.


.webp)
.webp)
.webp)